一文了解 LSM-Tree
什么是 LSM-Tree
SSTables 的结构
想要了解 LSM-Tree(Log Structured Merge Tree,日志结构合并树),我们得先了解 SSTables。SSTables 即排序字符串表(Sorted String Table),也是 LSM-Tree 里的核心数据结构。它的概念来自 Google 的 Bigtable 论文,大概的意思就是,SSTable 是一种可持久化,有序且不可变的键值存储结构,key 和 value 都可以是任意的字节数组,并且给提供了按照指定 key 查找和指定范围的 key 区间迭代遍历功能。
如下图所示,该图表示一个个日志结构存储数据段文件:为了避免最终用完磁盘空间,才将日志分为特定大小的段,对旧段文件进行压缩和合并,在新的日志文件中只保留每个键的最近更新。这种情况下,由于旧段的内容不会被修改,因此合并的段可以放入一个新的文件,旧段的合并和压缩都可以在后台线程完成,请求时仍然使用旧段处理,而完成合并后,就能直接删除旧段,使用新的合并段。
日志中稍后的值优先于日志中较早的相同键的值
怎么保证最近更新?
- 每个段都包含在一段时间内写入数据库的所有值。这意味着一个输入段中的所有值必须比另一个段中的所有值更新(假设我们总是合并相邻的段)。当多个段包含相同的键时,我们可以保留最近段的值,并丢弃旧段中的值
合并几个 SSTable 段,只保留每个键的最新值。此处每个段的键都是唯一的,是经过了一个压缩的过程
我们对这些段文件要求键值对的序列按键来排序,且保证每个键在同一个段文件中只出现一次(在压缩过程中已经保证了,只保留最近更新),此外,SSTable 具有内存索引。在 SSTable 的结构中,包含了若干的键值对,称为block,在其末尾,存储了一组元数据 block,记录数据 block 的描述信息,比如索引、BloomFilter、压缩、统计等信息,其中索引记录了这些数据 block 的键的偏移量。
An SSTable provides a persistent, ordered immutable map from keys to values, where both keys and values are arbitrary byte strings. Operations are provided to look up the value associated with a specified key, and to iterate over all key/value pairs in a specified key range. Internally, each SSTable contains a sequence of blocks (typically each block is 64KB in size, but this is configurable). A block index (stored at the end of the SSTable) is used to locate blocks; the index is loaded into memory when the SSTable is opened. A lookup can be performed with a single disk seek: we first find the appropriate block by performing a binary search in the in-memory index, and then reading the appropriate block from disk. Optionally, an SSTable can be completely mapped into memory, which allows us to perform lookups and scans without touching disk.
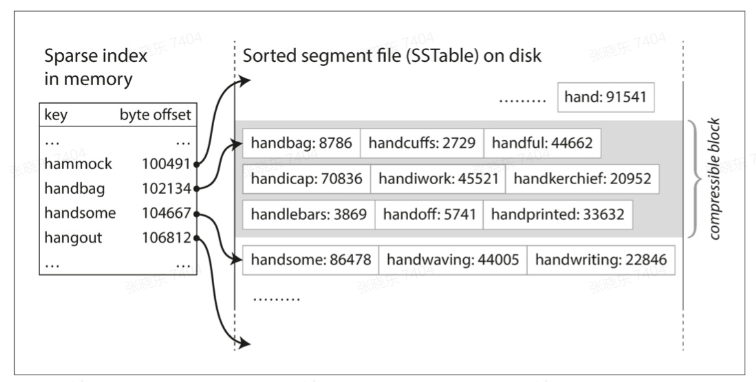
在文件中查找一个特定的键不需要保存内存中所有键的索引,如下图所示,如果要找键handiwork,但不知道段文件中该 key 的确切偏移量,但是你知道handbag与handsome的偏移,而且由于 key 有序的特性,你还知道handiwork在其二者之间。因此可以跳到handbag的位置开始扫描,直到扫描至handsome。索引记录了一些键的偏移量,虽然可能会很稀疏,但是由于扫描文件的速度很快,每几千个字节段文件有一个 key 索引就可以了。
由于 Read 请求需要扫描请求范围内的多个键值对,因此可以将这些记录分组到块中,写入磁盘前对其压缩,如下图灰色部分,索引的每个条目都指向压缩块的开始处,即节省了磁盘空间,也减少了 I/O 带宽使用
如果每个 key,value 都是等长的(容易获取记录分界点),甚至可以直接在段文件上二分查找,避免了使用内存索引
在下文 LSM-Tree 的结构中可以看到 SSTable 一般是分 level 的,level 级数越小,表示处于该 level 的 SSTable 越老,最大级数由系统设定。当某个 level 下的文件数超过一定值后,就会将这个 level 下的一个 SSTable 文件和更高一级的 SSTable 文件合并,由于 SSTable 是有序的,合并过程相当于一次多路归并排序,速度较快。Leveled-N 模型有着减小写放大作用。
LSM-Tree 的概念和结构
大致了解了 SSTables,下面我们来看看 LSM-Tree
LSM-Tree 是一种分层、有序、针对块存储设备特点设计的数据存储结构。它的核心思想在于将写入推迟 (Defer) 并转换为批量 (Batch) 写,首先将大量写入缓存在内存,当积攒到一定程度后,将他们批量写入文件中,这要一次 I/O 可以进行多条数据的写入,充分利用每一次I/O,从而实现高效地顺序写入数据。顺序写入的速度比随机写入的速度快很多,即追加内容,非就地更新,类似普通的日志写入方式以 append 的模式追加,不覆盖旧条目。
追加日志看起来很浪费,为什么不更新文件,以新值覆盖旧值?
顺序写入速度比随机写入快得多:追加和分段合并是顺序写入的操作,通常比随机写入快得多。某种程度上顺序写入在基于闪存的固态硬盘(SSD)上也是优选
- 当然,较于随机写的 B-Tree,LSM-Tree 的写入速度会更快,而 B-Tree 的读取速度更快,LSM-Tree 的读取速度比较慢。
易于处理并发和崩溃恢复:段文件(SSTable)是附加的或不可变的,不必担心在覆盖值的时候发生崩溃情况导致将包含旧值和一部分新值保留在一起
合并旧段可以避免数据文件随时间的推移而分散的问题
- 这里指的是随着使用时间变长,不断随机写入导致的磁盘碎片的问题
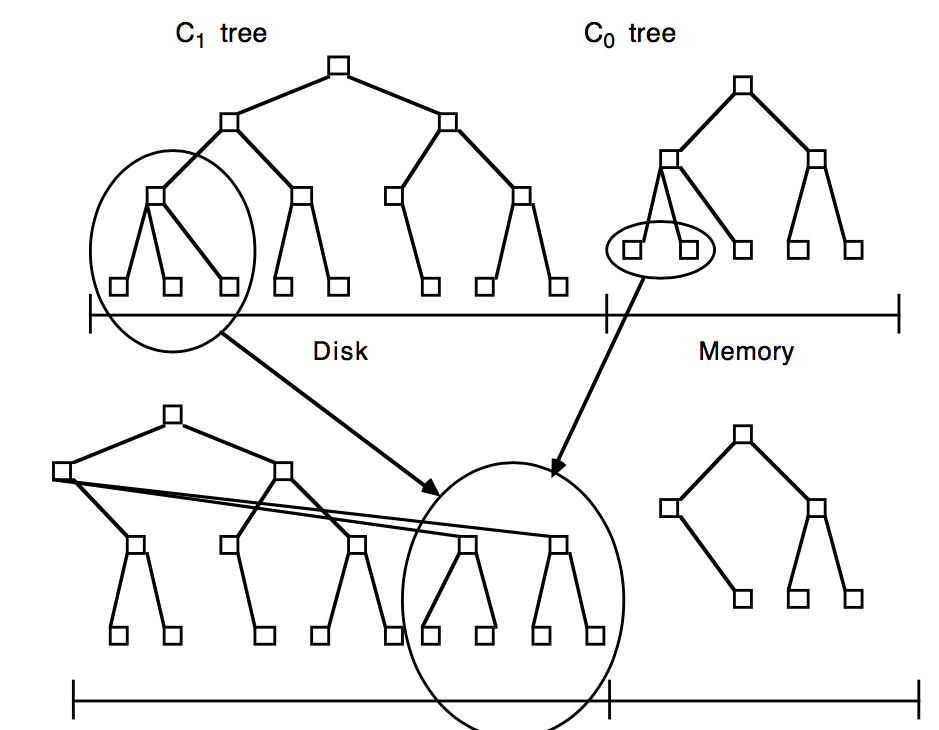
LSM-Tree 一般由两个或两个以上存储数据的结构组成,这些存储数据的结构也被称为组件(一般是多组件,只有 C0 在内存中,其余都在磁盘中),这里举个最简单的只有俩组件的例子,一个称为 C0-Tree,常驻内存中,可以是任何方便键值查找的数据结构,如 AVL 等结构,另一个称为 C1-Tree,常驻硬盘中,结构与 B-Tree 相似。C1 在初始时为空,当内存 C0 的大小到一定程度的时候就要进行rolling merge,C0 会将部分内容 dump 到 C1 中,将数据从小到大(从左到右)依次追加写到 C1 的一个 multi-page block 叶节点 buffer 中,如果 buffer 满了就将其写到硬盘,以此类推,直到 C0 扫描到最右,C1 首次产生。当然,C0 并不将所有的条目都拿来 rolling merge, 由于 C0 存储在内存之中,所以 C0 可以保留最近插入或最常访问的那些数据,以提高访问速率并降低 I/O 操作的次数,C1 中经常被访问的结点也将会被缓存在 C0 中。
LSM 在 merge 的时候如何把即将 merge 的数据定位到 C1 已经写入磁盘中的数据?
- LSM 在 merge 时可以从根结点开始逐级往下选取与 C0 的新数据最接近的数据,更加复杂的办法还可以考虑每次 C0 往 C1 merge 的数据的位置的频率
当存在以下情况时,C1 目录节点会被强制刷盘
-
包含目录节点的 multi-page block 缓存满了,只有该 multi-page block 会被刷盘
-
根节点分裂,增加了 C1 的深度,所有 multi-page block 被刷盘
-
checkpoint 被执行,所有 multi-page block 刷盘
rolling merge:可以想象为拥有一个概念上的游标,在 C0 和 C1-Tree 的等值 k-v 之间缓慢穿梭移动,将 C0 索引数据取出放在 C1-Tree 上
- 当增长的 C0-Tree 第一次到阙值
- 最靠左的一系列条目会以高效批量形式从 C0-Tree 中删除
- 然后被按 key 递增顺序重组到 C1-Tree,C1-Tree 会被完全填满
- 连续的 C1-Tree 的叶节点会按从左到右顺序,首先放置到常驻内存的 multi-page block 内的若干初始页上
- 直到该 multi-page block 被填满
- 该 multi-page block 被刷盘,称为 C1-Tree 叶节点层的第一部分,直接常驻硬盘
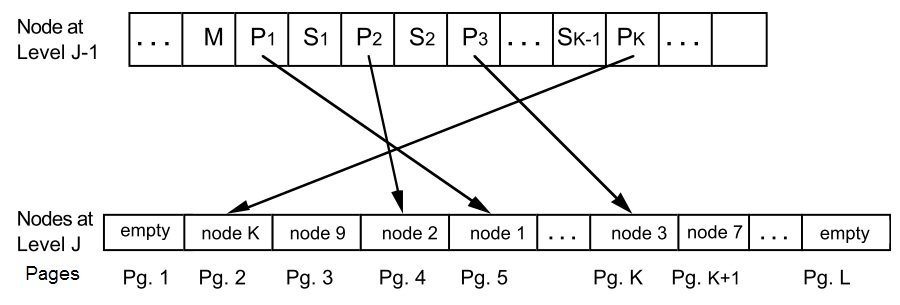
- 随着连续的叶节点不断添加的过程,C1-Tree 的目录节点会在内存缓存中被创建(为了高效利用内存和硬盘,这些上层目录节点会被存放在单独的页(或 multi-page block)缓存中,还有分隔点索引 M,将访问精确匹配导向某个下一层级的单页节点而不是 multi-page block。因此可以在 rolling merge 中使用 multi-page block,索引精确匹配时访问单页节点)
multi-page block:不同于 B-Tree,LSM-Tree 的延时写 (数据可以积攒) 可以有效的利用 multi-page block,在 rolling merge 的过程中,一次从 C1 中读出多个连续 pages,与 C0 进行 merge,然后一次向 C1 写回这些连续 pages,这样有效利用单次I/O完成多个 pages 的读写(B-Tree 在此场景下无法利用 multi-page 的优势)
batch:同样因为延迟写,LSM-Tree 可以在 rolling Merge 中,通过一次 I/O 批量向 C1 写入 C0 多条数据,那么这多条数据就均摊了这一次 I/O,减少磁盘的 I/O 开销
multi-page block 及其结点结构
rolling merge
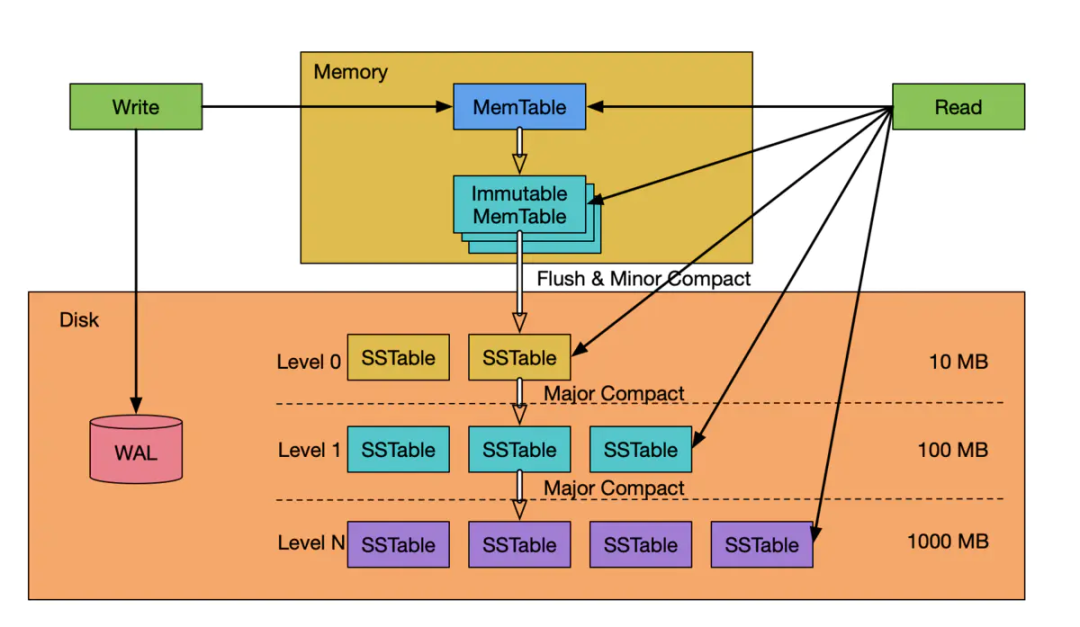
在上面的 LSM-Tree 结构图中,我们还看到了 WAL 和 MemTable,以及 Immutable MemTable。实际上,上图是 LSM 经过实践后形成的结构,LSM-Tree 的内存结构可以由一个 MemTable 和一个或多个 Immutable MemTable 组成。
-
MemTable 往往是一个跳表组织的有序的数据结构(也可以是有序数组或红黑树等二叉搜索树),即支持高效的动态插入数据,对数据进行排序,也支持高效的对数据进行精确查找和范围查找。
-
Immutable Memtable 是内存中只读的 MemTable,由于内存是有限的,通常会设置一个阙值,当 MemTable 占有内存到阙值后就会转换为 Immutable MemTable,与 MemTable 的区别在于它是只读的。它的存在是为了避免将 MemTable 中的内容序列化到磁盘中时会阻塞写操作
-
WAL 结构与其余数据库的一致,是一个只能在尾部以 append only 追加记录的日志结构文件,用于系统崩溃重启时重放操作,使得 MemTable 与 Immutable MemTable 未持久化到磁盘中的数据不会丢失。严格来说,WAL 并不是 LSM-Tree 数据结构的一部分,但是实际中,WAL 却是数据库中不可缺少的一部分。每当内存数据写到 SSTable 时,相应的 WAL 日志就可以被丢弃
应用场景与优劣
应用
LSM-Tree 是基于硬盘的数据结构,与 B-Tree 相比,能显著的减少硬盘磁盘臂的开销,并在较长时间内提供对文件的高速插入/删除,但在查询需要快速响应的时候性能不佳。通常 LSM-Tree 适用于索引插入比检索更频繁的应用系统,如日志系统,推荐系统,或者 no sql 数据库等,较为出名的有 Lucene search engine、Google Big Table、LevelDB、ScyllaDB、RocksDB 等等。
在大量应用服务上线的今天,每天都会产生大量的日志,需要存储下来便于服务监控、数据分析、排查定位问题和链路追踪等。在推荐系统中,也要每时每刻记录用户的行为信息,用于训练线上运行的推荐模型,且用户和内容的一些动态特征信息每天也要频繁更新,方便提供个性化服务。
优点
LSM-Tree 的主要优势在于能推迟写回硬盘的时间,进而达到批量地插入数据的目的
- 减少写放大
写放大:在数据库声明中写入数据库导致对磁盘的多次写入。在写入繁重的应用程序中,性能瓶颈可能就是数据库写入磁盘的速度:存储引擎写入次数越多,可用磁盘带宽内每次写入次数越少
B-Tree 必须至少两次写入每一段数据,即使一页中只有几个字节发生了变化,也需要一次编写整个页面的开销,而 LSM-Tree 的延时写能够充分利用每一次I/O ,一次 I/O 将多条数据写入,减少了写入磁盘的次数,有研究表明,LSM-Tree 能够在可用 I/O 带宽内提供更多的读取和写入请求
- 比 B 树支持更高的写入吞吐量
顺序写入紧凑的 SSTable 文件而不是必须覆盖树中的几个页面,其中顺序写入比随机写入快得多
- 可以更好的被压缩
B-Tree 存储引由于分割会留下一些未使用的磁盘空间,而 LSM-Tree 不是面向页面的,并且会定期重写 SSTables 以去除碎片,所以具有较低的存储开销
缺点
LSM-Tree 的缺点主要在于空间放大和读放大,以及压缩过程有时会干扰正在进行的读写操作:如果一项数据更新多次,这项数据可能会存储在多个不同的 SSTable 中,甚至一项数据不同部分的最新数据内容存储在不同 SSTable 中(数据部分更新),导致读操作繁杂。一项数据在磁盘中存储了多份副本,老的副本是过时无用的,导致数据实际占用的存储空间比有效数据需要的大,即空间放大。在查询某个具体数据的时候,需要按新到老的顺序查找 SSTable,直到找到所需的数据。如果目标数据在最底层 Level-N 的 SSTable 中,则要读取和查找所有的 SSTable,即读放大问题。
对于空间放大问题,可以通过类似GC(即压缩,只保留最近的 key,删除旧数据或标记为已删除的数据) 的过程来解决。而针对于读放大,也可以通过分层和布隆过滤器解决。
分层即 SSTable 的 Level 机制,可以限制查找的范围。
- 每个 level 中都是上个 level 归并下来的,在单个 level 不会有重复 key。当数据量到达一定程度后会归并到下一个 level。比如 level1 的第一个文件大到临界值,会和 level2 的文件进行归并,去除了该文件与 level2 文件的重复 key,保证了 level2 不会有重复 key。
- level0 是在内存中 dump 下来的,不能保证没有重复 key。内存中维护了一个活跃内存表 MemTable 和一个不变内存表 Immutable MemTable,用于区分何时将 c0 数据结构 dump 到磁盘(超过一定大小触发),不变的内存表又易于 dump 数据。二者相互交替,周期性的将不变内存表 dump 到内存中形成一个分段文件。
布隆过滤器可以快速确定数据在不在 SSTable 中,避免了数据不存在时,遍历 SSTable 读取数据 block 内容带来的开销。当然,有还是会极少部分因为有冲突导致穿透,但这完全可以接受,因为数据不存在的数据在布隆过滤器中一定不存在。
在 WiscKey 中,还将读写分离与 LSM 相结合进行优化,不但减少了读写放大,延长 SSD 使用寿命,还充分利用了 SSD 的并行读写特性(线程池随机异步读写)。它的 SSTable 中不再存储 value,而是存储指向 value 的指针,避免了当 value 很大时,多次归并 SSTable 需要多次移动 value 降低性能。value 与 WAL 结合为 vLog,vLog 中也存储了 key 可以同时用于崩溃恢复。
实现及操作
构建 LSM-Tree 的整个流程中,如何让数据按键来排序呢?答案是在内存中来维护,因为在内存中维护总是比在磁盘中维护有序结构容易得多
- 写入数据时,将其添加到内存中的平衡树数据结构,即内存表 MemTable
- 当内存表大于某个阈值(通常是几兆字节)的时候,将其作为 SSTable 文件写入磁盘中。新的 SSTable 则成为数据库的最新部分,当 SSTable 被写入磁盘时,会开一个新的 MemTable 继续写入数据
- 为了提供读取请求,会先在 MemTable 找到该关键字,然后在最近的磁盘段中,在下一个较旧的段中找到该关键字
- 有时会在后台运行合并和压缩来组合段文件并丢弃或覆盖旧值
- 同时需要在磁盘中保存一个单独的日志(WAL)来记录每个写入,防止数据库崩溃时,未写入磁盘的 MemTable 的数据丢失。该日志仅有的作用就是崩溃后恢复 MemTable
- 更新
更新即插入,在读取时总是从 C0-Tree 到 Level0 的 SSTable 到更老的 SSTable,总是能读取到最新值
- 删除
为了更高效地利用 LSM-tree 的插入优势,删除操作被设计为通过插入操作来执行。当要删除一个条目时,先在 C0 上找对应的索引是否存在,如果不在就建一个索引,在索引键值上设置删除条目,通知所有访问该索引的操作该条目已删除。后续滚动合并中,在较大 CxTree 中碰到与该索引键值相同的条目都将被删除。在 C0 查找该条目时,碰到该删除条目,会直接返回未找到。如果 C0 上找到该索引存在,则直接将删除条目覆盖该索引
参考
Be the first person to leave a comment!